どうしてロープの速さが場所によって違うのか
倍力で荷を引く時、ロープがある所では速く、ある所では止まったように見えます。どうしてこんなことが起きるのでしょうか。これは動滑車を使用しているからです。動滑車の前後で、ロープの速さに荷の速さ分が加わることが原因しています。
ではどれぐらい速さが異なるのでしょうか。クイズ形式で解説をしたいと思います。
2倍力の場合

まずは一番単純な2倍力からです。
こんな具合に荷を引く場面を想像してみてください。
いきなりクイズですが、荷が引っ張られる速さaが1だとすると、bとcのそれぞれの場所でロープのスピードはどうなるでしょうか。選択肢①~③の中で正しいのはどれでしょうか。
| ① | ② | ③ |
|
b=1 c=1 |
b=0 c=1 |
b=0 c=2 |
正解は③です。
bでは端が固定されているため速さはゼロです。cでは動滑車を跨いでいるので、荷の速さの2倍分が加算されますので、速さは2になります。
しかしそもそも2倍分が加算されるのはどうしてでしょうか。

動滑車の前後のロープだけに注目してみてください。荷が移動するにともない、動滑車は同じ分だけ移動します。すると、動滑車の後ろ側で1の分のロープが、動滑車の後ろ側で1の分のロープが巻き取られることになります。動滑車の後ろ側で荷の速さの2倍分が加算されるのはこういうわけです。
3倍力の場合
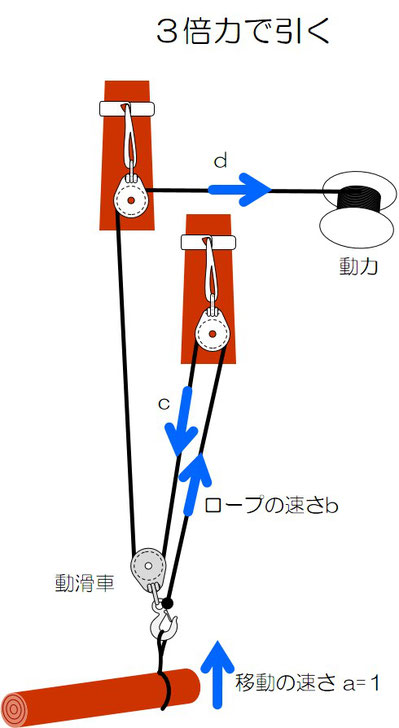
では倍力を増やしてみましょう。3倍力の場合はどうなりましょうか。
次の選択肢の中で正しいものはどれでしょうか。
| ① | ② | ③ | ④ |
|
b=0 c=1 d=3 |
b=0 c=1 d=3 |
b=1 c=1 d=3 |
b=1 c=3 d=3 |
正解は③です。
bは荷と同じ速さで動きますので、ゼロではなく1になります。
また定滑車の前後でロープの速さは変わりませんので、b→cで速さは同じなので、④はありえません。
4倍力の場合

では4倍力ではいかがでしょうか。
速度変化のパターンが掴めてきたと思いますが、次の選択肢の中から正しいものを選んでください。
| ① | ② | ③ |
|
b=0 c=2 d=2 e=4 |
b=1 c=2 d=3 e=4 |
b=1 c=3 d=3 e=4 |
正解は①です。
動滑車の前後で2づつ加速するのが正解です。
定滑車の前後では加速しませんので、cとdは同じです(②は不正解)。
d→eも動滑車の前後ですから、dと3の速度差は2になります(③は不正解)。
5倍力の場合

5倍力で最後にしましょう。
次の選択肢の中から正しいものを選んでください。
| ① | ② | ③ | ④ |
|
b=0 c=0 d=2 e=2 f=4 |
b=0 c=0 d=2 e=2 f=4 |
b=1 c=1 d=3 e=3 f=5 |
b=1 c=2 d=3 e=4 f=5 |
正解は③です。
bは荷に固定されていますので、荷と同じ速さ1になります(①、②は不正解)。
また定滑車の前後で速さが変わることはありませんので、④も不正解です。
おわりに
以上のとおりですが、倍力を使うと、単純にロープの末端(動力側)の速さは倍力数分だけ速くなります。2倍力なら2、3倍力なら3というように。ロープが倍数に比例して長くなる分、動力にかかる力の大きさは反比例して小さくなります。このことを知っているだけでも十分かもしれません。
(参考)倍力を標準機能にした搬器
森の機械 架線用搬器 HANAKO A2 は荷の吊り上げを1倍力(倍力なし)~3倍力の間で行うことができます。
今回は、途中のところのロープの速さに注目してみました。実際にお使いになっている方は感覚的にお気づきだと思いますが、具体的な数字で解説してみました。しかし速さが飛び飛びで増えていくのは驚きだったかもしれませんね。
よろしければ現場でこうした倍力の仕組みをお使いの方は、お確かめになってみてください。
お付き合いいただきありがとうございました。
関連動画
本ブログより後に作成したYouTube動画です。(2023年6月5日撮影)
実際のロープの動きが分かりますのでどうぞご覧下さい。